- 이동평균/지수이동평균선
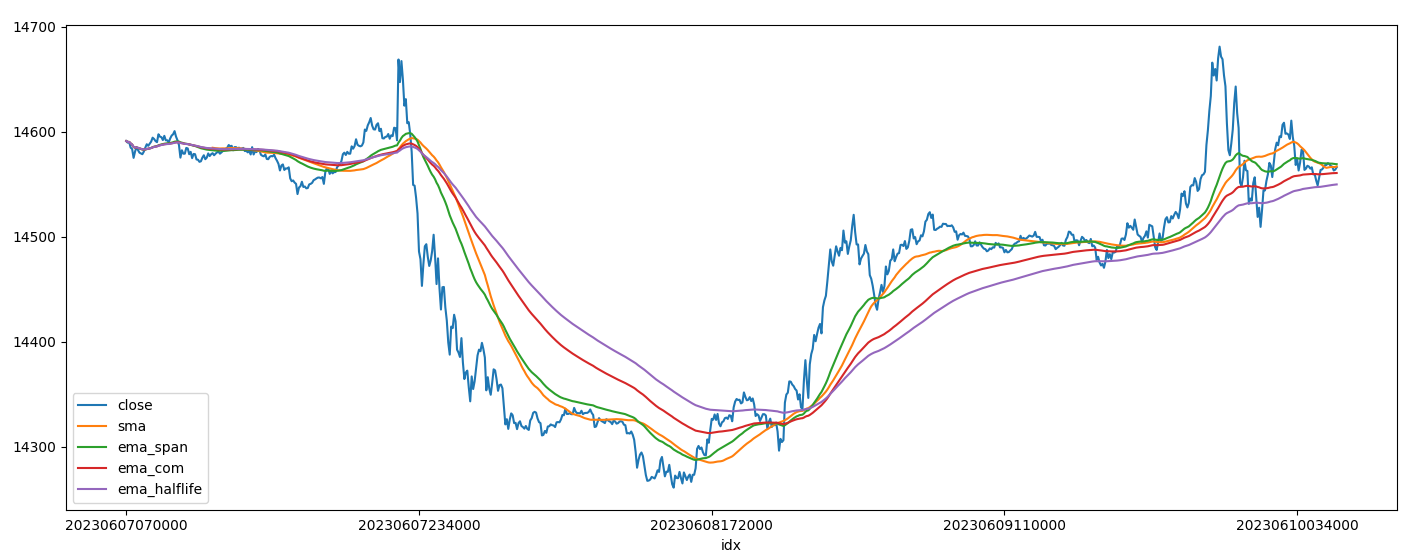
# 이동평균/지수이동평균(span/com/halflife)
df['sma'] = df['close'].rolling(tf).mean()
df['ema_span'] = df['close'].ewm(span=tf).mean()
df['ema_com'] = df['close'].ewm(com=tf).mean()
df['ema_halflife'] = df['close'].ewm(halflife=tf).mean()
큰 변동성 없이 상승하거나 하락하는 경우에 그럭저럭 쓸만하다. 단순이동평균보다는 지수이동평균이 조금 더 빠르게 움직이기 때문에 성과가 더 좋을 것 같지만 가끔은 단순이동평균의 계산대상이 되는 기간을 변경하는 것이 오히려 더 효과적일 때도 있다.
- 특정 기간 동안의 최저점

# 특정 기간 동안의 최저점
df['simple_low'] = df['low'].rolling(tf).min()
가격의 방향이 완전히 바뀌는 시점에 청산하는 방법인데 지난 저점이라는 것은 너무나도 명확한 가격이기 때문에 투자자들의 Stop Loss가 많이 걸려있는 가격이라 트랩에 빠지는 경우가 많았기 때문에 Average True Range를 살짝 가감해서 조정하는 것이 좋은 듯하다.
- YOYO / CHANDLIER 청산

# Average True Range 계산
df['tr'] = np.where(df['high'] - df['low'] > df['high'] - df['close'].shift(1), df['high'] - df['low'], df['high'] - df['close'].shift(1))
df['tr'] = np.where(df['tr'] > df['low'] - df['close'].shift(1), df['tr'], df['low'] - df['close'].shift(1))
df['atr'] = df['tr'].rolling(tf).mean()
df.drop(['tr'], axis=1)
# YOYO / CHANDLIER (ATR X 3)
df['yoyo (close - atr x 3)'] = df['close'] - df['atr'] * 3
df['chandlier (max(high) - atr x 3)'] = df['high'].rolling(tf).max() - df['atr'] * 3
Average True Range를 활용하는 다른 대표적인 두 가지 방법인데 Chandlier 청산은 지난 고점을 어떻게 설정하느냐가 까다롭지만 Yoyo 청산은 메인이 되는 다른 청산 방법에 부가해서 보험적인 성격으로 사용할 때 성과가 좋았다.
특정 기간 동안의 최저점을 청산방법으로 설정하는 것을 개인적으로 선호하는 데 이 경우 제일 큰 문제가 짧은 기간 동안 변동성이 집중되어서 수익이 발생하는 경우 청산가격은 여전히 낮은 곳에 위치해 있기 때문에 시장의 변화를 빠르게 감지하지 못한다. (물론 빠르게 변하는 변동성에 맞춰서 청산가격을 올려주는 것이 모든 전략과 상황에서 성과가 개선되는 효과가 있는 것은 아니겠지만...)
유리한 가격의 변동성을 청산가격에 어떻게 반영할 수 있을까 고민하다가 최저점 가격대에다가 최근 가격의 표준편차와 ATR의 특정 배수를 곱한 가격을 더하는 방법을 생각해 봤다.
- 특정기간 동안의 최저점 + 종가의 표준편차 X 배수

# 특정기간 동안의 최저점 + 종가의 표준편차 X 배수
df['simple_low'] = df['low'].rolling(tf).min()
df['low + std(close) x 1'] = df['simple_low'] + df['close'].ewm(span=tf).std() * 1
df['low + std(close) x 2'] = df['simple_low'] + df['close'].ewm(span=tf).std() * 2
이 경우 우측에 급격한 상방 변동성이 나왔다가 다시 크게 하락하는 경우 기존의 청산방법(최저점)은 청산가격의 변화가 거의 없지만 표준편차를 더한 청산방법의 경우 청산가격이 종가의 상방 변동성을 따라서 빠르게 증가하는 흐름을 보여준다.
- 특정기간 동안의 최저점 + ATR * 배수
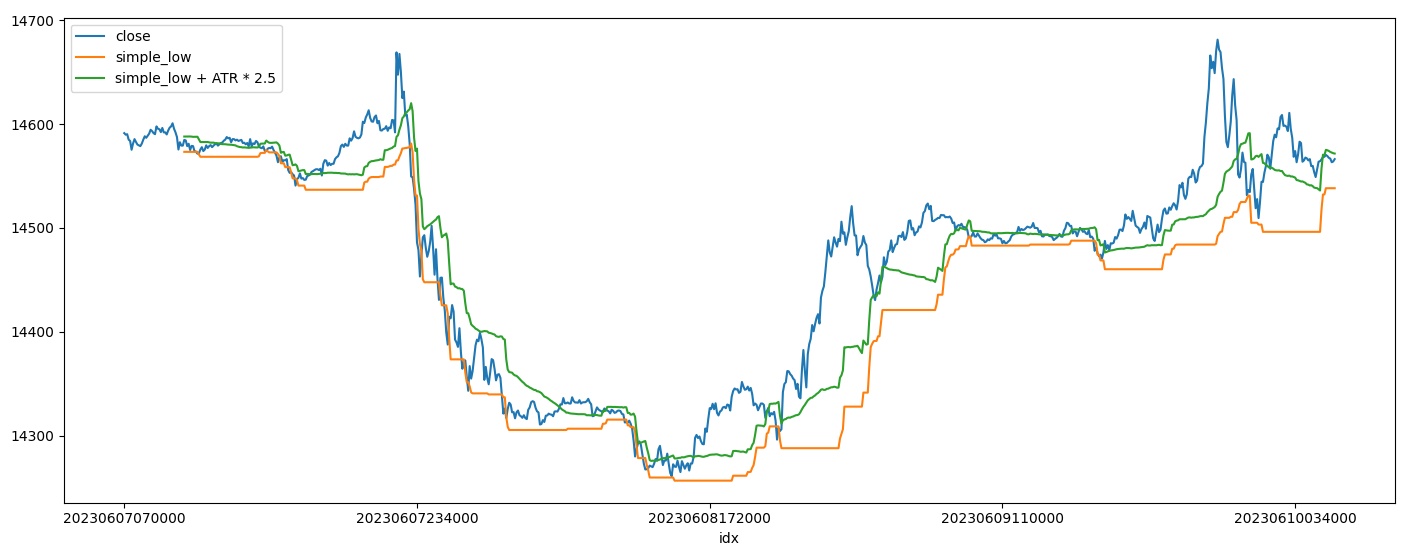
# Average True Range 계산
df['tr'] = np.where(df['high'] - df['low'] > df['high'] - df['close'].shift(1), df['high'] - df['low'], df['high'] - df['close'].shift(1))
df['tr'] = np.where(df['tr'] > df['low'] - df['close'].shift(1), df['tr'], df['low'] - df['close'].shift(1))
df['atr'] = df['tr'].rolling(tf).mean()
df.drop(['tr'], axis=1)
# 최저점 + ATR * multiple
df['simple_low + ATR * 2.5'] = df['simple_low'] + df['atr'] * 2.5
위 표준편차를 활용하는 방법과 기본적인 개념은 같다. 표준편차를 고려할 때도 기간과 배수를 함께 고려해야 되는 것처럼 Average True Range의 기간 설정과 배수 등을 적절하게 설정해줘야 한다.
'시스템트레이딩' 카테고리의 다른 글
| 몇가지 짧은 생각 (0) | 2023.07.25 |
|---|---|
| lower high - lower low 역추세 전략 (NQ/ES) (0) | 2023.07.24 |
| DAX 선물 거래시간 (0) | 2023.06.14 |
| Drawdown에 대한 고민과 해결방법 (0) | 2023.06.13 |
| 국내 파생상품 개장시간 변경예정 (09:00 -> 08:45) (0) | 2023.06.09 |


